Как выбрать форму кулачковой кривой зум-объективов?
На заключительном этапе проектирования зум-объектива необходимо спроектировать кривую кулачка. Чтобы сбалансировать равномерность изменения увеличения изображения и угла поворота кулачка, необходимо выбрать подходящую форму кривой кулачка и установить определенную функциональную взаимосвязь между увеличением изображения M и углом поворота кулачка θ.
В соответствии с фактическими граничными условиями и непрерывностью функции, которой должна соответствовать кулачковая кривая, устанавливаются несколько общих функциональных отношений между M и θ, а примеры проектирования моделируются с помощью Matlab.
Результаты показывают, что когда установленное соотношение степенной функции между увеличением изображения M и углом поворота кулачка θ и углом подъема давления не превышает допустимого значения, баланс изменения переменного увеличения является лучшим, кривая изменения увеличения является плавной и нет точки перегиба кулачка. Этот метод может помочь дизайнерам изменить форму кривой кулачка в соответствии с различными требованиями дизайна и найти лучшую кривую кулачка масштабирования.
В системе масштабирования кулачок является компонентом, который управляет движением группы линз и позволяет системе изменять фокусное расстояние, сохраняя при этом плоскость изображения стабильной. Плавное, гибкое и быстрое масштабирование является важной составляющей производительности масштабирования, которая напрямую связана с шероховатостью профиля кулачка и углом давления кривой кулачка.
Если кривая кулачка имеет больший угол наклона на определенном участке, она кажется более крутой. В процессе вращения кулачка возникает ощущение тяжести в руке. Шестерня, приводящая во вращение кулачок, изношена, а край канавки кулачка может даже быть сдавлен и деформирован, что влияет на качество изображения; в более серьезном случае камера застрянет и ее вообще невозможно будет использовать.
В зум-объективе с механической компенсацией путем выбора соотношения движения между перемещением группы зуммирования и углом кулачка можно добиться того, чтобы увеличение изображения изменялось с одинаковой скоростью или с равномерным ускорением во время процесса масштабирования. Это очень многообещающе, будь то телевидение, пленочная фотография или зум-объективы, используемые в военной разведке.
Но при этом угол давления, соответствующий кривой кулачка на обоих концах длинного и короткого фокусных расстояний, будет очень большим. При миниатюризации зум-объектива крутящий момент кулачка часто превышает допустимое значение. Поэтому необходимо выбрать форму кривой кулачка и найти баланс между равномерностью изменения увеличения изображения и углом поворота кулачка.
В этой статье установлена зависимость степенной функции между увеличением изображения M и углом поворота кулачка θ. В сочетании с уравнением системы масштабирования интерфейс моделирования Matlab написан для моделирования формы кривой кулачка. Результаты показывают, что установленная функция M-θ более линейна, чем традиционная аппроксимация кривой и метод θ-x, кривая кулачка более плавная, угол подъема давления в целом меньше (<45 °), а изменение увеличения более сбалансировано. .
Основная теория системы масштабирования
Завершающий этап проектирования зум-объектива, то есть после того, как определены параметры оптического механизма (радиус, интервал, материал стекла) каждого элемента объектива, необходимо также рассчитать числовую зависимость между смещением зум-группы и компенсацией. группу для обработки кулачковой дорожки. Ниже мы обсудим две формы уравнения кривой кулачка.
Форма 1: Получите величину перемещения y группы компенсации из величины перемещения x группы переменного увеличения, а затем получите кривую кулачка переменного увеличения, а именно
х→у→м2* ,м3* →М (1)
Форма 2: Получите увеличения m2* и m3* группы переменного увеличения и группы компенсации из переменного увеличения M, требуемого системой, и получите перемещение x, y группы переменного увеличения и группы компенсации, а затем получите кривая кулачка, а именно
М→м2*, м3*→x,y (2)
Из двух приведенных выше форм видно, что для того, чтобы составить уравнение кулачка и затем обработать траекторию кулачка, необходимо установить функциональную связь между углом кулачка и одной из вышеупомянутых переменных.
Проектирование кривой кулачка масштабирования
Чтобы сбалансировать равномерность изменения увеличения изображения и угла кулачка, необходимо выбрать подходящую форму кривой кулачка. Это требует от нас установления определенной функциональной зависимости между увеличением изображения M и углом поворота кулачка θ, о чем речь пойдет ниже.
1. Официальное обсуждение
Сначала укажите следующие символы.
ж1, е2, е3, е4: Это фокусные расстояния передней фиксированной группы, группы масштабирования, группы компенсации и задней фиксированной группы;
м2,м3: Соответственно боковое увеличение группы масштабирования и группы компенсации;
м23= м2м3: Боковое увеличение части переменного увеличения, состоящей из группы переменного увеличения и группы компенсации;
м230:Горизонтальное увеличение части с переменным увеличением в начальной точке (θ=0) в фокальном положении. В этом примере показано положение с самым коротким фокусным расстоянием;
L: максимальное перемещение группы масштабирования;
θ: Угол поворота кулачка;
α: максимальный угол поворота кулачка;
R: Радиус барабана:
M: Увеличение масштаба;
Макс. Максимальное увеличение;
x,y: соответственно представляют величину перемещения группы масштабирования и группы компенсации;
Среди них к.Икси кдапредставляют собой наклоны группы масштабирования кривой кулачка и группы компенсации соответственно, то есть значение тангенса их угла подъема давления.
При построении функциональной связи между θ и M необходимо обратить внимание на два граничных условия:
Первое граничное условие: когда θ=0°, M=1.
Второе граничное условие: когда θ=α, M=Mmax.
(1) θ имеет линейную связь с M
Это может привести к тому, что изменение увеличения приведет к равномерному эффекту, это соотношение можно выразить как
Приведенную выше формулу можно использовать для дифференцирования θ и получения скорости изменения увеличения:
(1) Существует линейная зависимость между θ и M
(a) Сначала постройте зависимость степенной функции между θ и M:
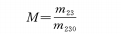
M: Увеличение масштаба;
ММакс: Максимальное увеличение;
x,y: соответственно представляют величину перемещения группы масштабирования и группы компенсации;
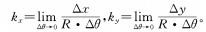
Среди них к.Икси кй— это наклоны группы масштабирования кривой кулачка и группы компенсации соответственно, то есть значение тангенса их угла подъема давления.
При построении функциональной связи между θ и M необходимо обратить внимание на два граничных условия:
Первое граничное условие: когда θ=0°, M=1.
Второе граничное условие: когда θ=α, M=Mmax.
(1) θ имеет линейную связь с M
Это может привести к тому, что изменение увеличения приведет к равномерному эффекту, это соотношение можно выразить как

Приведенную выше формулу можно использовать для дифференцирования θ и получения скорости изменения увеличения:
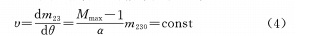
(1) Существует линейная зависимость между θ и M
(a) Сначала постройте зависимость степенной функции между θ и M:

В формуле М, ММакс, α, θ определяются, как указано выше, n — коэффициент кривой кулачка, который также можно рассматривать как коэффициент регулировки, и указывается n≠0. (5) Дифференцируя формулу по θ, можно получить:
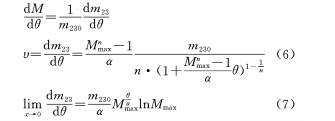
(б) Постройте показательную функцию зависимости между θ и M
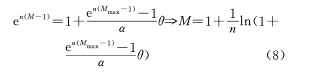
Формулу (8) можно получить, дифференцируя θ:
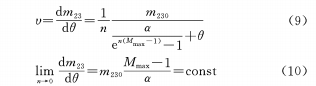
(c) Постройте логарифмическую функцию зависимости между θ и M
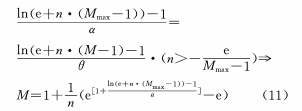
После дифференцирования существует
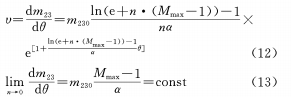
(d) Построить зависимость функции Гаусса между θ и M
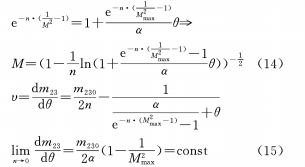
(д) Четыре приведенных выше функциональных зависимости используются в случае n≠0. Для случая n=0 оговорим:

То есть существует линейная зависимость между θ и x, которая в настоящее время является наиболее часто используемой зависимостью. Продифференцировав уравнение (16) и уравнение кулачка, получим скорость изменения увеличения как
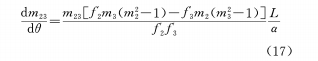
Вышеуказанные результаты обсуждаются ниже.
(1) Когда θ имеет линейную зависимость от M, из формулы (4) видно, что переменное время системы и равномерная скорость очень желательны. Однако из-за нелинейной зависимости между величиной перемещения x группы масштабирования и М это неизбежно приведет к неравномерности скорости перемещения группы линз и дисбалансу угла давления.
(2) Когда θ и M находятся в нелинейной зависимости, а θ и M находятся в зависимости от резервной функции, если n постоянно, переменное увеличение и угол поворота будут меняться в зависимости от резервной функции. Из формулы (7) видно, что при приближении коэффициента кривой кулачка n к 0 переменное увеличение и угол поворота изменяются экспоненциально, то есть увеличение увеличивается все быстрее при вращении кулачка.
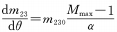
При n=1 и выполнении условий приведенной формулы скорость изменения увеличения является фиксированной величиной, то есть за все время вращения кулачка от конца наименьшего фокусного расстояния до конца наибольшего фокусного расстояния. , изменение увеличения является равномерным, что соответствует ситуации, обсуждаемой в формуле (4).
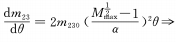
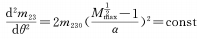
Когда m=1/2 и выполняются условия приведенной выше формулы, изменение увеличения происходит равномерно ускоренно, чего мы и ожидаем.
(3) Связь между θ и M является экспоненциальной, логарифмической и гауссовой. Когда n постоянно, скорость изменения увеличения обратно пропорциональна θ, то есть, когда кулачок постепенно вращается от наименьшего фокусного расстояния до самого длинного фокусного расстояния, скорость изменения увеличения становится все медленнее и медленнее.
Когда n изменяется, скорость изменения увеличения нелинейна по отношению к кривой θ. Когда коэффициент n кривой кулачка приближается к 0, скорость изменения увеличения является постоянной, то есть изменение увеличения является линейным.
Вообще говоря, принцип выбора кривой кулачка заключается в выборе формы кривой с наилучшим переменным изменением увеличения и кривой плавного изменения увеличения, когда угол подъема давления не превышает допустимого значения.
Благодаря приведенному выше обсуждению и экспериментальному моделированию в Matlab мы понимаем, что когда связь между θ и M является резервной функцией, путем выбора соответствующего коэффициента регулировки n можно добиться того, что, когда угол давления близок к допустимому значению, переменная Изменение увеличения имеет лучший баланс и изменение увеличения. Кривая плавная, точек перегиба кулачка нет.
Однако ни одна из других функций не может достичь лучших результатов. На рисунке 1 представлена схема моделирования кулачка, разработанная с использованием программного обеспечения для трехмерного рисования на основе результатов предыдущего анализа. Ниже описаны результаты наших симуляционных экспериментов.
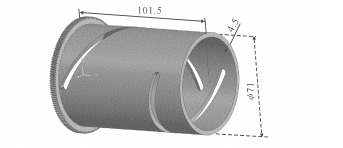
Рис. 1. Модель кулачка.
2. Анализ и моделирование
Объедините две формы методов решения кулачковых кривых, приведенные выше, и функциональную связь между θ и M, чтобы скомпилировать графический интерфейс Matlab.
Входные параметры программы:
Коэффициент кривой кулачка n, короткое фокусное расстояние оптической системы f0, фокусное расстояние группы переменного увеличения f2, фокусное расстояние компенсационной группы f3, упреждение (дистанция перемещения группы переменного увеличения от короткого фокусного расстояния к длинному фокусному расстоянию) wl, объекты в группе переменного увеличения на коротком фокусном расстоянии, расстояние l20, расстояние изображения компенсационной группы составляет ll30на коротком фокусе максимальный угол поворота кулачка α, интервал углов поворота mu в угловых единицах и диаметр кулачкового барабана dd.
Выходные параметры программы:
Угол поворота, перемещение группы масштабирования, перемещение группы компенсации, фокусное расстояние, угол подъема давления группы масштабирования, угол подъема давления группы компенсации, а также данные и графики коэффициента масштабирования.
С помощью этого программного интерфейса вы можете легко увидеть взаимосвязь между коэффициентом масштабирования и углом поворота, наблюдать, превышает ли угол подъема давления допустимое значение, и изменить коэффициент регулировки, чтобы быстро изменить вышеуказанное соотношение и найти наилучшую требуемую кривую кулачка. .
Возьми 20ИксСистема положительной компенсации непрерывного масштабирования, разработанная исследовательской группой в качестве примера для выбора кривой кулачка.
Фиксированные параметры:
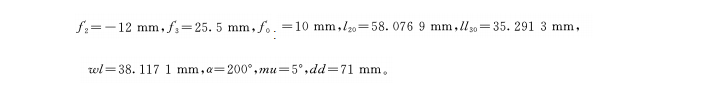
Переменный параметр: коэффициент корректировки n
В этой программе можно редактировать все вышеперечисленные параметры. Чтобы облегчить обсуждение, здесь мы главным образом рассмотрим влияние поправочного коэффициента n на результат.
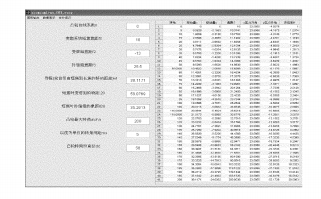
Рис. 2 Интерфейс моделирования Matlab
(1) Когда n=0, существует линейная зависимость между θ и x, как показано на рисунке 3.
(2) Когда n = 0,047, график степенной функции показан на рисунке 4.
(3) При n= 0,000 1 график показательной функции показан на рисунке 5.
(4) При n= 2,32 график логарифмической функции показан на рисунке 6.
(5) При n = 0,1 график функции Гаусса показан на рисунке 7.
Эксперимент доказывает, что предыдущее обсуждение взаимосвязи различных функций соответствует тренду кривой графика.
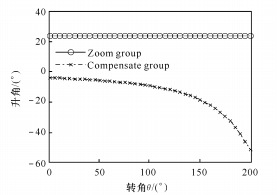
(а) Зависимость между углом подъема давления и углом поворота
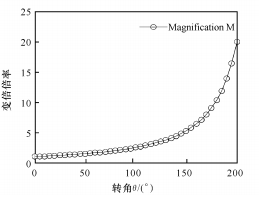
(б) Связь между коэффициентом масштабирования и углом поворота
Рис. 3. Линейная зависимость между θ и x
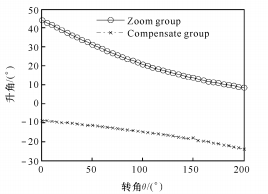
(а) Зависимость между углом подъема давления и углом поворота
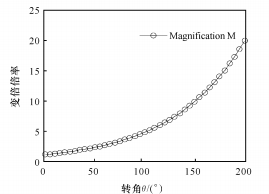
(б) Связь между коэффициентом масштабирования и углом поворота
Рис. 4. Степенная функция между θ и M
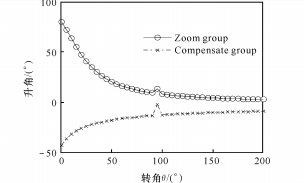
(а) Зависимость между углом подъема давления и углом поворота
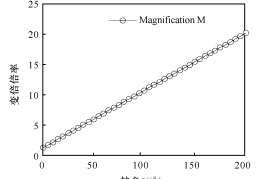
(б) Связь между коэффициентом масштабирования и углом поворота
Рис. 5 Показательная функция между θ и M
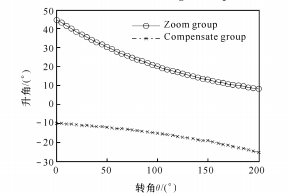
(а) Зависимость между углом подъема давления и углом поворота
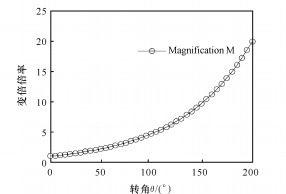
(б) Связь между коэффициентом масштабирования и углом поворота
Рис. 6. Функция логарифма между θ и M.
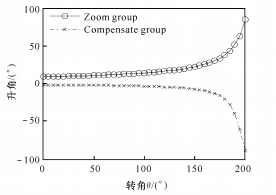
(а) Зависимость между углом подъема давления и углом поворота
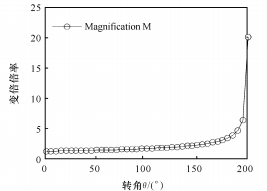
(б) Связь между коэффициентом масштабирования и углом поворота
Рис. 7. Функция Гаусса между Q и M
Анализ приведенного выше примера кратко иллюстрирует влияние различных значений коэффициента регулировки n на результаты расчета кривой кулачка, и соответствующая модификация параметров может привести к лучшим результатам.
В ходе испытаний было установлено, что когда n принимает определенные конкретные значения, общий угол давления кривой кулачка соответствует требованиям, и только в определенной точке внезапно превышает разумное значение. Такую точку мы часто называем точкой перегиба кривой, когда кулачок вращается. Когда он достигает определенного угла, он внезапно не может продолжать вращаться, то есть застревает в машине.
Это губительно как для конструкции кулачка, так и для эффекта масштабирования, поэтому при проектировании следует избегать кривых с такими точками перегиба. То есть необходимо провести несколько испытаний, чтобы гарантировать получение разумного коэффициента корректировки.
В то же время, может ли определенное значение коэффициента регулировки оптимизировать кривую кулачка, зависит от требований к диаметру кулачка, углу давления кривой кулачка, который он может выдержать, требованиям к общему углу поворота кулачка. , объем и вес системы, а также требования к скорости масштабирования.
Таким образом, метод проектирования, определяющий уравнение кривой кулачка масштабирования коэффициента регулировки, может помочь разработчикам гибко изменять кривую, чтобы они могли изменять форму кривой кулачка в соответствии с различными проектными требованиями и находить лучшую кривую кулачка масштабирования.
Случайным образом извлеките несколько положений масштабирования из приведенных выше экспериментальных данных и приведите их к коду V, чтобы убедиться, что поверхность изображения стабильна, а качество изображения соответствует проектным требованиям.
3. Результаты экспериментов
Согласно приведенному выше анализу и моделированию, кулачок зум-объектива, который мы разработали, был успешно применен, как показано на рисунке 8. После проверки полевых фотографий кулачок, разработанный с использованием вышеуказанной теории в зум-объективе, имеет быстрое и плавное масштабирование, точное компенсационная кривая, хорошее качество изображения в разных фокусных точках и полностью соответствует расчетным показателям, что подтверждает правильность приведенного анализа.

Рис. 8 Зум-объектив
Выберите соотношение степенной функции между θ и M, и, изменив поправочный коэффициент n, можно будет найти различные компромиссы между линейной зависимостью между θ и x и линейной зависимостью между θ и m23, что не только гарантирует, что угол подъема давления будет не быть слишком большим, но также избегать серьезной неравномерности скорости изменения скорости.
Конечно, чтобы получить линейную зависимость θ-m23 или θ-dm23/dθ, вы можете увеличить угол α или увеличить диаметр кулачкового барабана, чтобы уменьшить максимальный угол подъема давления на кривой кулачка, но это увеличить объем и вес объектива. Уменьшение фокусного расстояния компенсационной группы также уменьшит максимальный угол подъема давления на компенсационной кривой.
Это усложнит структуру фиксированной группы и даже снизит качество оптической схемы. Следовательно, выбор соотношения степенной функции между θ и M может помочь нам оптимизировать кривую кулачка и разработать миниатюрный высококачественный зум-объектив.
Если после прочтения приведенного выше содержания вы хотите получить дополнительную информацию о зум-объективе, вы можете связаться с Quanhom для получения комплексного решения.
Как профессиональный производительОптико-электромеханические компонентыИмея многолетний опыт, Quanhom располагает профессиональной командой исследований и разработок и строгой системой контроля качества. Наши различные тепловые инфракрасные линзы (ЛВИР,МВИРи камеры SWIR) продаются по всему миру и получили похвалу и доверие многих клиентов. Мы во всем ставим потребности клиентов на первое место и можем предоставить клиентам продуманные индивидуальные услуги. Если вы хотите купить наш инфракрасный объектив с непрерывным зумом, немедленно свяжитесь с нами!
Авторы: Ян Лэй, Цзя Пин, Хун Юнфэн, Ван Пин
Источник журнала: Том 31 № 6 Журнал прикладной оптики, ноябрь 2010 г.
Дата получения: 25 марта 2010 г. Дата редакции: 23 июня 2010 г.
Использованная литература:
[1] ТАН Цзянь-бин. Оптимизированная конструкция контура кулачка с переменным фокусом [J]. Optical Technique, 1994, 20(1): 27–29 (на китайском языке с аннотацией на английском языке).
[2] ЧЖАН Сю-ли. Новый метод улучшения контура кулачка компенсирующей линзы [J]. Юнгуан Техник, 2003, 35 (2): 16-17. (на китайском языке с аннотацией на английском языке)
[3] Цуй Цзюнь, Х.Э. Го-Сюн. Подходящая конструкция контура кулачка зум-объектива [J]. Китайский журнал научного инструмента, 1990, 11 (1): 107–112. (на китайском языке с аннотацией на английском языке)
[4] Группа разработчиков кинообъективов. Оптическая схема объектива для киносъемки [ M ]. Пекин: Китайская отраслевая издательская компания, 1971 г. (на китайском языке).
[5] ЧАН Цюнь. Корпус оптических расчетов [М]. Пекин: Science Publishing Company, 1976. (на китайском языке).
[6] Цуй Цзи-чэн. Конструкция рефракционно-отражательного зум-объектива с большой апертурой [J]. Оптика и точное машиностроение, 2008? 16 (11): 2087–2091. (на китайском языке с аннотацией на английском языке)
[7] ДОН Ке-ян, ПАНЬ Ю-лун, ВАН Сюэ-джин и др. Оптическая схема инфракрасной двухдиапазонной системы ступенчатого масштабирования HDE [J]. Оптика и точное машиностроение, 2008, 16 (5): 764-770. (на китайском языке с аннотацией на английском языке)
[8] ХАО Хун-юнь, СЮН Тао. Средневолновая инфракрасная оптическая система с двойным полем зрения [J]. Оптика и точное машиностроение, 2008, 16 (10): 1891–1894. (на китайском языке с аннотацией на английском языке)
[9] ЧЭНЬ Синь, Фу Юэ-ган. Оптимальная конструкция кривой кулачка для системы масштабирования [J]. Журнал прикладной оптики. 2008, 29 (1): 45-47. (на китайском языке с аннотацией на английском языке)
[10] Сюй Чжэн-Гуан, Чжао И-Фей, СОН Цай-Лян и др. Оптимизация конструкции кривой кулачка с масштабированием с помощью OZSAD[J]. Журнал прикладной оптики, 2006, 27 (3): 203-207. (на китайском языке с аннотацией на английском языке)
[11] МЭН Цзюнь-хэ, ЧЖАН Чжэнь, СУНЬ Син-вэнь. Оптимизация камеры зум-объектива [J]. Инфракрасная и лазерная техника, 2002, 31(1): 51-54. (на китайском языке с аннотацией на английском языке)
